Patterns From Pentagrams

A watercolor by Margi Lake of the Ghurid Portal pattern, Herat, Friday Mosque .

© Margi Lake, used with permission

The tradition of Islamic geometric ornament is a family of beautiful patterns but they come to us without instructions. The search for layout solutions is two part; we seek to reproduce them in various media but we also seek to understand them. Reproducing one pattern is useful, but understanding the deeper basis of pattern designs is more satisfying as it unlocks entire families of pattern. The main purpose of this website is the second; the purpose is to understand the larger families and see the deeper relationships of pattern.

Some patterns contain obvious clues to their structure and construction; they obviously relate to one of the Euclidean or Archimedean tilings. Some more complex families of pattern require a familiarity with the traditional treatment of themes, such as in rosettes. Some patterns give up their secrets more reluctantly.

This analysis looks at a surprising, early, example of a family containing apparently regular pentagons in a symmetry which does not involve 5 or 10 fold divisions. It appears to be a simple 4 fold symmetry pattern. It is not possible to define a regular pentagon using a 4/8 fold or 12/24 fold division. Some close approximations are possible in the higher numbers of circle divisions, but it often appears that the pentagons are truly regular polygons. I believe that we have, in this early example, a pattern based on a very simple division of the circle which contains clearly regular pentagons.

The Ghurid Portal Herat. © tobeytravels used with permission

This Ghurid pattern from the Friday mosque at Herat is surprisingly complex for its early date. This example appears on the “Ghurid portal”, created around 597 AH/1200 CE.**  This pattern appears, at first glance, to be a simple case. It is obviously a square repeat tiling and it even has the octagon and square Archimedean tiling marked out with glazed center medallions. A huge number of patterns are formed by placing a star polygon at the centers or vertices of a Euclidean, an Archimedean, or some other semi- regular tiling. Six point stars typically occur at hexagonal tiling vertices; eight point star occur at square and octagon vertices.

What is remarkable about this case is that almost nothing about this pattern is simply derived from the four or eight fold tiling. The solution to the pattern is only found when the family of angles is studied; all pattern angles derive from the pentagram vertex angle. The star polygon placed at the vertices to create this pattern is the pentagram with angles unrelated to the tiling symmetry.

**Hansen, Eric, Najimi, Abdul Wasay, Christensen, Claus, Hansen, Inger Kickan, The Ghurid Portal of the Friday Mosque of Herat, Afghanistan. Aarhus University Press, 2015. ISBN: 9788771249132 8771249133

2. The origin of the central star polygon angles

An attempt to understand a pattern like this is an attempt to fit a construction to a photograph. We have only the result to work from. We are fortunate to have a very well preserved pattern in this case. It allows a careful analysis of the angles and proportions. Everything that follows is, of course, personal opinion but it is the fourth or fifth attempt at understanding this pattern and by far the simplest approach. It also fits with a very large family of patterns which can be created this way. A simple star polygon mapped onto the vertices of a perfect tiling.

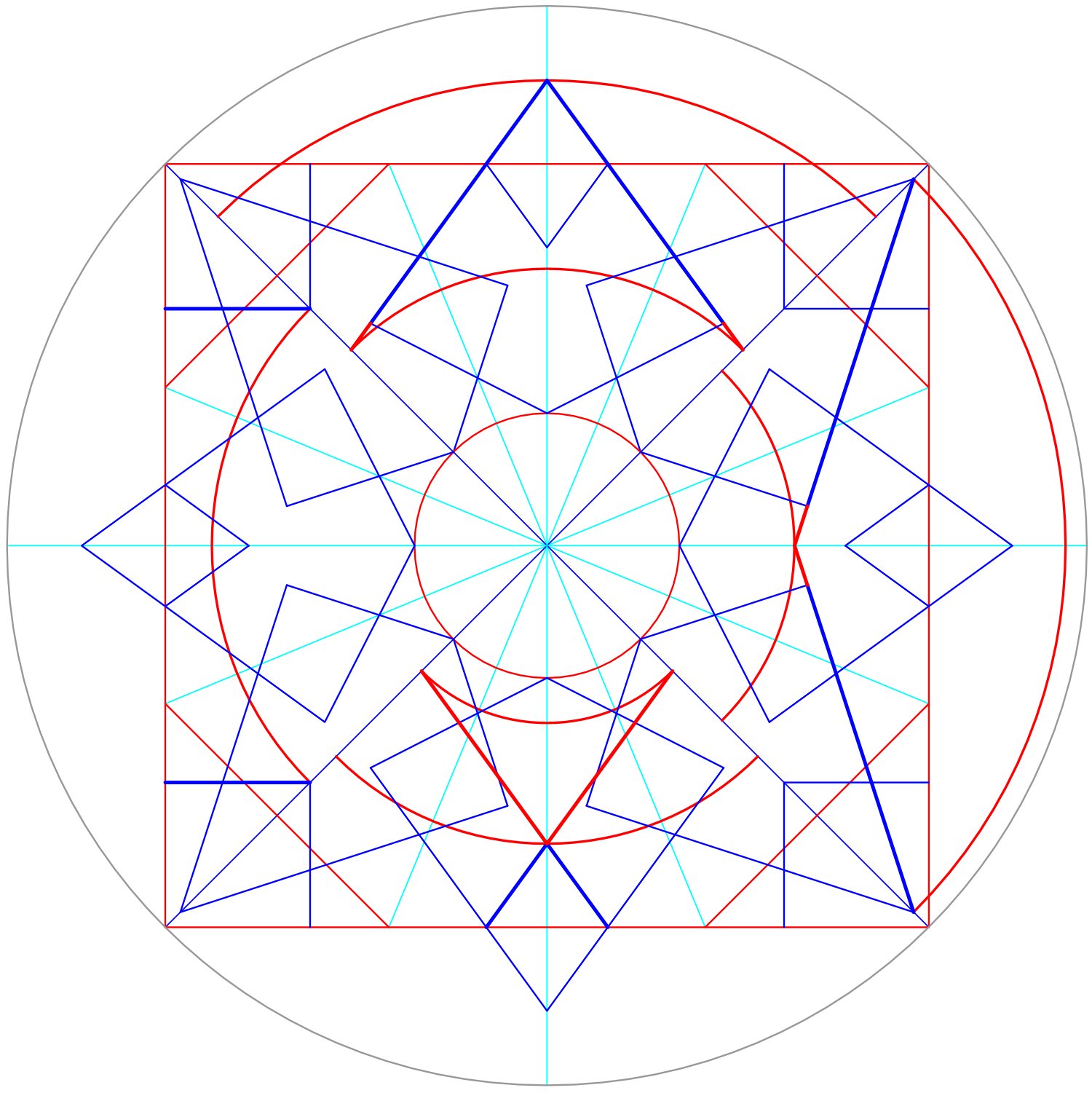
The basis of this pattern is obviously the Archimedean octagon plus square tiling, helpfully identified here by the blue glazed medallions. The first problem is that the angles of the center star polygon are unusual. The source of these unusual angles is a pentagram. A pentagram inscribed in the octagon defines two new layout circles. The two layout circles define an unusual 8 star polygon with the apex angle of the pentagram.

3. A center star polygon with unusual angles.

The remainder of the pattern is formed by pentagons and the pentagram figures which define them. Eight pentagrams plus the center star of Fig. 3 form an almost complete definition of the pattern.

Regular pentagons can only appear in an eight fold tiling if they are either completely contained inside the tiling or, as in this case, their symmetry line sits on the tiling edge. As a result, the pentagrams’ five fold divisions do not align with the eightfold division so each pentagram is defined individually in its divided circle.

One of the reflection symmetry lines of the pentagrams must be aligned to the tiling edge here, but the scaling of those pentagrams, the radius of the layout circle in Fig. 5, is a choice by the artist. The first radius of this pentagram construction is the very common choice of a radius equal to the side of the polygon tile, the octagon. A further scaling step was added here as in Fig 5. The reason for the choice may be a surprising deeper layer of design to be shown below in Fig. 12. The center star polygon and the single pentagram drawn in in Fig. 6 already show an almost complete definition of the full 1/8th pattern.

The remaining seven pentagram centers can be drawn individually but each circle would need to be divided separately. This is a fairly painful way to draw a pattern like this.

The pattern can be completed more economically by transferring the new pattern lines, shown in the bottom of Fig. 8, around the layout.

Fig. 4. The pentagrams are centered on each vertex of the octagon. Their scaling is not obvious.

Fig. 5. The pentagram layout circle is inscribed in a pentagon aligned to the tile edge as shown

Fig. 6. The scaled pentagram and the basic structure of the pattern

Fig. 7 Trimming the pentagram at the tiling edge and where it crosses the center 8 star polygon pattern lines

Fig. 8 Two pentagrams are required to complete each quarter pattern. The resulting pattern lines are shown at the bottom of the figure

The pentagram symmetry is unrelated to the fourfold symmetry of the overall pattern but so long as the pentagrams centers respect that fourfold symmetry their sides can be completed without drawing every pentagram in its divided circle.

The top of Fig. 8 shows the layout with each pentagram drawn out but, as shown in the bottom of the figure, only six pattern lines need to be transferred around the layout. These can be transferred by extending a pair of pattern lines to the quarter divisions of the layout and treating each pair of pattern lines as a four point star polygon as in Fig. 9. This polygon can then be defined by two layout circles.

Fig. 9 Defining pattern lines as four point stars for layout

The same analysis for each pair of pattern lines, extended to define a four fold star polygon, is shown in Fig. 10.
The corner squares in the left quadrant of Fig. 10 require only one layout circle since they are known to be parallel to the divisions by construction, they are the extensions of a square.

The complete set of layout circles required to transfer the pentagram lines around the layout is shown in Fig. 11. The layout is kept manageable by drawing in each pair as needed.

Fig. 10 Pairs of layout lines as fourfold stars

Fig. 11 All layout circles. This looks untidy but it is still cleaner than 8 pentagram layouts.

Only one additional layout element is required. The tips of the kites oriented to the diagonal corners are untidy. They terminate too close to each other when tiled. This is commonly solved by turning the pattern into an interlaced crossover pattern. The required layout is simple as shown in the corners of Fig. 11.

Tiling 1. A unit cell of the wall pattern as constructed

Tiling 1 shows the pattern as executed for the Ghurid Portal including the rather peculiar choices of interlace. I have rearranged the unit cell to be centered on the 8 star here. The original structural unit is easily seen in the original photograph. It is centered on the square and “bowties”. These units were probably made as described by Sarre **.

Some of the pattern elements show relatively poor symmetry due to the interaction of the five and eight fold elements. The kites, or almonds, at the vertices of the center 8 star polygon have, in fact, no symmetry plane. This is quite clear in the very well executed terra cotta original and cannot be cured in this pattern where the pentagrams align to the tile edge. Peculiar symmetry elements like this are often clues to the original structural concept.

** The large pattern was assembled from square unit tiles. A probable method of production is described in Friederich Sarre, Denkmäler persischer Baukunst Bd 1, page 10. It is a summary of Eduard Jacobsthal, “Mittelalterliche Backsteinbauten zu Nachtschewan im Araxesthale”, Deutsche Bauzeitung, Bd 33, 14 Oct. 1899, Nr 82, 1899. Pages 513-516. Nr 83, Illustrations 10 & 11page 521, Nr 84 pages 525 - 528, Illustration 5 page 529. Nr 88, pages 549 - 551, Nr 91 pages 569 - 574. Particularly page 569. Hathi Trust Digital Library, www.hathitrust.org.

Tiling 2. Conventional interlace with the heavy elements found at Herat. On the right, a more typical pattern

Another unusual element of the pattern is clearest in the thinner interlace of Tiling 2 above. The kites around the center, regular, eight star polygon are of two types. The pattern is A, B, A, B around the unit cell. This is a result of the fact that the symmetry line of the pentagon is not aligned to the divisions of the center star polygon. We will see several patterns later where the pentagon symmetry line is aligned to the center star for perfect symmetry in the kites.

One final question remains regarding this pattern. Why was that specific scaling used for the pattern pentagram? The answer is probably found in Fig. 12. The pentagram inscribed in the smaller circle shows an exact relationship to the radius of the original circle. The radius of the incircle shown is exactly one quarter of the radius of the original layout circle, one quarter of the side of the octagon.

This is not a common pattern but very few patterns of any kind survive from before the Mongol arrival in the area. Examples** of this pattern are found at the Malik i-Zuzan madrasa, badly degraded, and a relative in stucco is found at the Palace of the Termez Shahs. 

A surprising number of closely related patterns do survive. They will appear here as I get them written up.

** Malik-i-Zuzan Madrasa See Archnet, Image ICA0043 in higher resolution. Badly degraded, bottom right of pillar.
Palace of the Termez Shahs, See Deniké, B, Les “Nouvelles Découvertes au Turkastan”, Cahiers d'art 1, 1930, pp. 41 -44 Fig 9. See also Uzgen (Ozgön) Mausolea, Kyrgyzstan for probably the same pattern. Column flanking portal, Southern tomb, 1186 CE. Archnet.

Fig 12 The proportioning of the original pentagram

This is a very fun family and understanding it pays huge dividends when studying more complex patterns such as the Mamluk woodwork of the minbars and kursi of Cairo.
Expect more fun stories. AA