Basic Operations with the Compass 3: Divided Circles. The Foundations of Geometric Pattern

There seem to be as many ways to draw any given pattern as there are experienced geometers to draw it. Every person is a product of years of study and experience and each of those roads took a slightly different path.

Some people look at Islamic pattern as a product of polygon tilings, as discussed by Hanbury Hankin and Jay Bonner. We will meet those in passing. Some people discuss them as the product of grids, a very similar way to view pattern. Some people view each pattern as a unique product of defined points on an elaborate base figure. My path leads me to an understanding of patterns based almost exclusively on Divided Circles. All of these methods are equally valid if used correctly. You are reading my version so you get my view here.

The development and proportioning of the repeating elements of the pattern are the second part of the art of Islamic Pattern. The first part is the division of the circle.

A pdf version of this page is found here. This web page will not print well.

One possible destination- A base layout for a ten fold pattern.

Fig 1. What lies beneath. The 20 fold division of the circle.

This introduction collects many of the common operations of the division of the circle and polygon construction in one place. The illustrations used here were created with a drafting program. They comply, however, with the traditional rules of compass and straight edge geometric construction. They could have been drawn with compass and straight edge. Computers are faster.

—

This website deals with geometric pattern, but currently has a heavy emphasis on Islamic star patterns- tiled simple star polygons and complex rosettes. These have several layers. Historical patterns very often show a layer of complex biomorphic design which enriches the pattern. It is related to, but not intimately linked to, the underlying geometry. It sits above the geometric interlace. In contrast, all of the geometric pattern layers are tightly related structures based on progressively deeper geometric foundations. We see the final pattern lines, often as interlaced designs. We usually do not see the underlying structural layout of the patterns in the finished work. Only very rarely do we see the deepest layer in the final pattern, the divisions of the circle which provide the foundation of it all. This summary introduces the creation of those divisions of the circle, without which geometric pattern cannot exist.

All repeating patterns, not only star pattern, depend at their roots on the divided circle. The divisions of the circle define the fourfold, fivefold, sixfold and higher symmetries and create the pattern by interacting with the layout we create through added radial structures, pattern layout circles. In many cases this is obvious, in some cases less obvious. Patterns which appear to depend only on a “grid” are also defined by the divided circle. Grids are drawn based on divided circles. It is not possible to discuss the foundations and drawing of Islamic geometric pattern without a good understanding of this basic material.

This document attempts to answer the questions- how are the divisions of the circle accurately and efficiently drawn? Constructions are presented for the common symmetries of pattern; 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 16 and 20 fold. These discussions will also, as a bonus, construct the exact Compass Constructible Polygons: 3, 4, 5, 6, 8, 10,12, 16, 20 and 24 sides . Some discussions will be added in another post for the cases where a specific size and orientation is needed, as for constructing a figure with a specific side dimension. Only the exact divisions and two approximate divisions are presented here. There are many more approximate constructions not mentioned.

Coincidentally these exact methods are likely to be the same methods used by historical artists; geometry has not changed in the last 3,000 years.

[Terms which appear in italics are defined in the “Glossary” under “Links Artists and Tutors > FAQs.”]

The Basics Of Circle Divisions; The First Division. Twofold.

Almost all Islamic star figures are radial symmetry figures; their symmetry is based on the circle. A divided circle is needed to construct the star. The divided circle does not appear in the final figure, but it is the foundation. All of the regular polygon constructions will also start with a divided circle. So what is a divided circle? If you have drawn a circle on a line, you have drawn a divided circle. A circle on a line is divided into two equal sectors. This is a one half division. A four fold division is “one forth”, a tenfold division is “one tenth”. These names rather than degrees were used to refer to the divisions, and sectors, by the Greeks. Any division can be properly named as a fractional division. Some common divisions cannot be named in precise degrees. A sevenfold division is for example, a 51.42857142857….. degree division.

The divided circle may start with a line. When we put our steel point of the compass on that line, we define [o], the origin or center of the circle. When we strike a circle from [o], the circle cuts the line at two new points [A] and [B]. We have a divided circle. It gets more complicated from here but this is almost always where we start.

For labeling of the figures, the letters will restart with each new section, or I would rapidly run out of letters. Points [A], [B], [C], and [D] will remain the same. I will drop the label for [o], the origin, as it gets crowded. [o] is always the origin, the center of the master, first, circle.

For an Islamic star figure we usually want to construct a layout circle with a set size. That size can be defined by a project or simply how much room we have on the paper. If the required layout measurement is the length [AB], it will be a diameter of our divided circle. The constructions will start with a circle of radius ½ of [AB], Radius [oA].

You can’t do much with a twofold divided circle. It is a basis rather than a destination. The next construction is the most natural division of the circle, and probably the most common symmetry of star patterns.

[See Notes 1 at the bottom for a curiosity of the naming of divisions.]

i) The Equilateral Triangle, the Hexagon: The Natural Divisions of the Circle

One of the most remarkable and useful observations of geometry is the relationship of the radius of a circle to the whole circle. If we start at a point, for example [A] and mark off its radius [oA] on the circumference of the circle, it will fit exactly 6 times around the circle. This is easy to prove but it always surprised me at first sight. It is very useful in drawing, carpentry machine work and of course, theory.

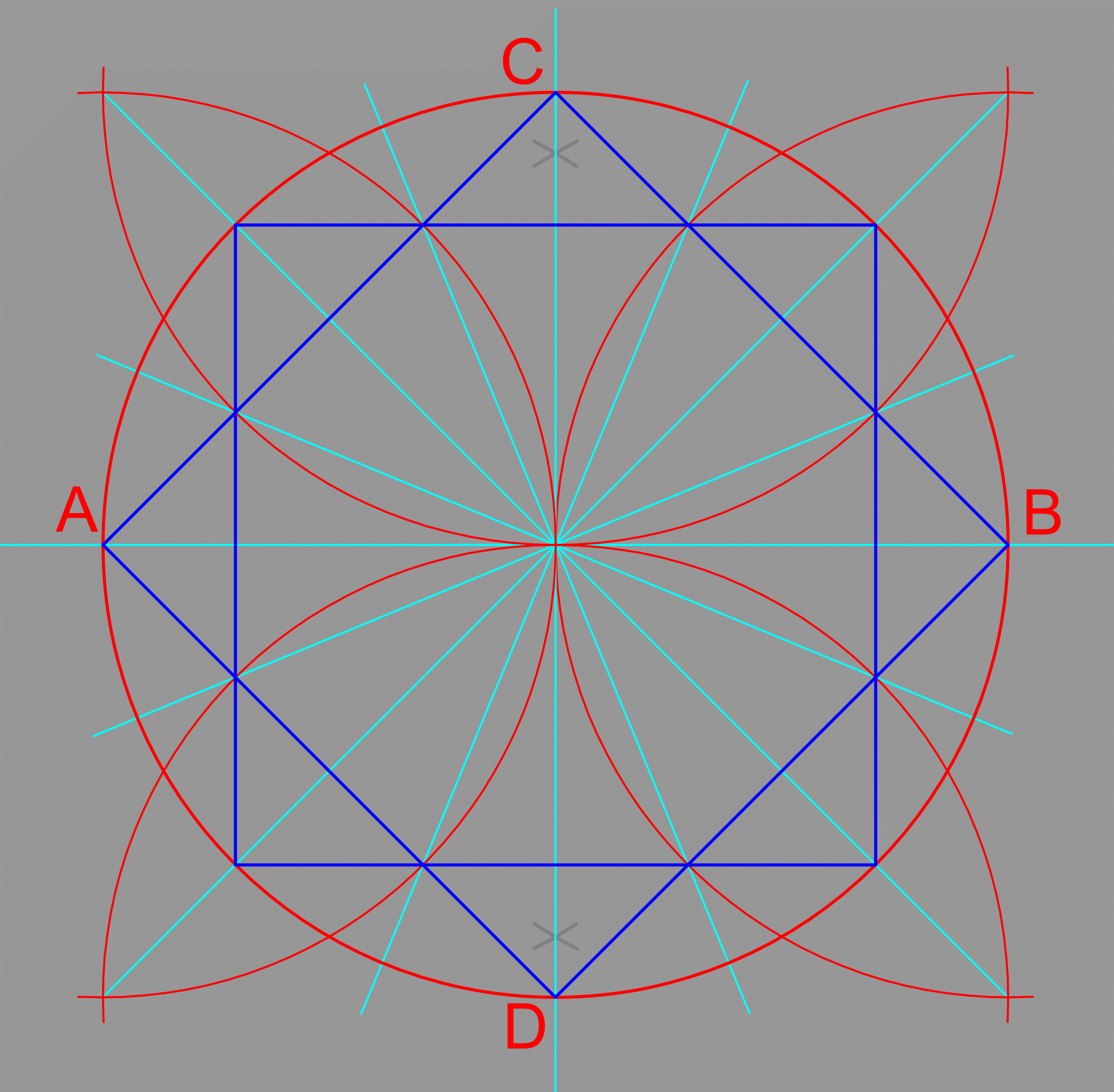
Starting with the twofold divided circle, a circle of radius [oA] on line [AB], we construct the sixfold division by marking an arc of radius [oA] from [A] and the same radius [oA]=[oB] from [B]. Where the arcs cut the circle, we have a sixfold division. The distance [EG] and [FH] are also equal to [oA].

A single compass setting perfectly divides the circle by identifying points [E], [F], [G] and [H]. Connecting the points across the circle, we have 6 radii, or three diameters, defining the six fold division. Connecting the adjacent points, [A] to [E], etc. creates the hexagon, our first regular polygon. Each radius is a radius of both the circle, and the polygon. It seems strange that we jumped straight from the circle on a line to sixfold division but the natural relationship of the radius to the circle means that it is the most intuitive and useful division.

We also created the three fold division in this layout. Connecting every other division will give one of two triangles, [AGH] or [BEF]. Notice that this triangle still creates six divisions if we extend the radii [oA], [oG] and [oH] across the circle. All odd polygons; triangle, pentagon, heptagon etc, create twice as may divisions as they have vertices directly. This construction is how we create the isometric grid, the endless grid of equilateral triangles. A field of tangent circles as large as desired is set up and the grid is drawn as a field of triangles, tip to tip.

There are two more odd polygons, heptagon and nonagon. These will be treated last as special cases since they have no exact compass and straight edge construction solutions. All of the remaining common polygons which are met in Islamic geometric art share a factor of four. Moving from the two fold to the four fold is the next step.

ii) The Fourfold Divisions and Multiples of Four

Many of the common circle divisions and their polygons share a factor of four in their count; fourfold and the square, eight fold and the octagon, 12 fold and the dodecagon, 16 fold and the hexadecagon, sometimes called the hexakaidecagon and 24 fold division and the 24 sided polygon the icosikaitetragon. The fourfold base is the key to all of these. A new division needs to be added to the circle on a line. The required new element is a perpendicular bisector of line [AB].

This is the first place where we meet the real world limits of an instrument. To the limits of your compass, bigger is better in layout circles. Larger circles usually allow more accurate location of intersections and lines. How they cross also matters, but in general bigger is better.

The textbook method to erect the bisector is shown in Fig 6. A new arc, radius [BA], is drawn from [B] to[A] and a second of the same radius from [A] to B]. Two new points, [X] and [Y] are identified. Connecting them gives a perpendicular bisector and the four fold division of the circle. The only problem is that, even on A3 paper, the circle [oA] is already getting large for most 6 inch (150 mm) compasses. (See Notes, 2) Since it is the very foundation of your pattern, this construction needs to be accurate. Compass extensions don’t work very reliably. You also want to keep your compass set at the radius [oA] for later layout work. Changing the radius and resetting it back to [oA] is less accurate. You need two compasses for this layout and you really need a beam compass. Most people do not have one. If you do have one, this is the best method. Bigger is better if you have the instruments, and the paper space.

A construction which does not need a second compass or a huge paper space is shown in Fig 7. Before circle [oA] is drawn, a circle [oW] is used to mark two points [W] and [X]. This radius should be a bit smaller than half of what you will use for [oA]. Now when you use radius [oA] to draw arcs from [W] and [X] to define [Y] and [Z] you get the result in fig 8 to define line [YZ].

A nice neat fourfold division of the circle. These four points, [A] to [D], are used to divide the circle further into 8, 10, 12, 16, 25 and higher divisions. It is very important to make these early stages as accurate as you can.

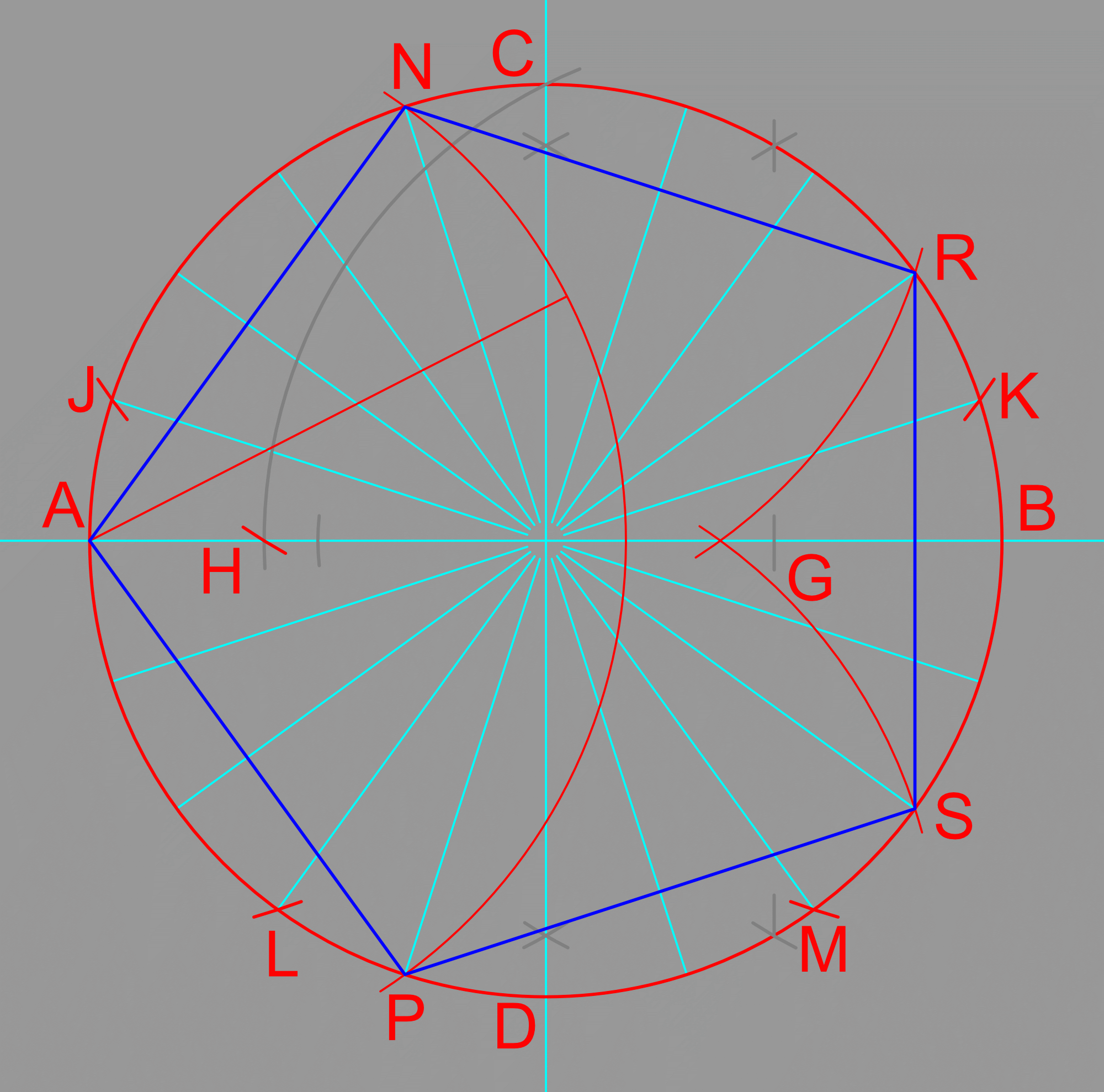
The next division is the most versatile. Drawing arcs from [A], [B], [C] and [D] with the original circle radius, [oA] we get figure 9. This now divides the circle into 8 divisions, where lines [EH] and [FG] cross the original circle, as well as 12 fold where the red arcs cross circle [oA].

As a further bonus, Fig 10 also already contains the elements of the 16 fold division. The crossing of the two squares in Fig 10 define a new set of 8 divisions but the intersection of the squares is not very well defined, it is a relatively flat crossing. The same crossing of the divisions at the two square is defined by the red arcs crossing the either one of the squares, and they cross one of them at 90º. We use the square which crosses the arcs at 90º. Figure 11 shows the economical result using the fourfold result square interacting with the eightfold layout arcs to create the 16 fold division.

Using only the arcs crossing the circle [oA] in Fig 12 shows the 12 divisions. In this case, the crossing of the two resulting hexagons would also define the next 12 divisions, for 24, but the intersection is even less well defined. It is better to use the diagonals [EF] and [GH] to draw a new set of divisions. Points [H], [J], [K], and [L] are used to draw the two new 6 fold divisions. The first set from[H] and [L] are drawn in Fig 13.

Your divisions should look like “Fig 14… Yes” after completing the divisions from [J] and [K]; a nice neat division into 24 parts. Resist the temptation to draw in the circles as in “Fig 14… No”. It’s cute but it makes a mess for later work.

At this point we have 3, 4, 6, 8, 12, 16 and 24 divisions. The most common remaining set of divisions are 10 and 20. They require a significant amount of work beyond the eightfold division.

iii) Factors of Five; Ten and 20 Fold Divisions.

Perhaps surprisingly, the division of the circle into five starts at Fig 8, the division into four. Only one of the points [A] through [D] appear in the final divisions but we need both line [AB] and point [C].

Divide your circle into four as for Fig 8 and draw a new arc from [B] through [o] to identify [E] and [F]. Find the point where line [EF] crosses [AB] and mark point [G] in Fig 15. You do not need the line, just the point. This is the reason that the choice of that original circle to define [W] and [X] was chosen back at Fig 7 as about- but not equal to- one half of the master circle radius. Point [G] is exactly half of line [oB]. We don’t want this point crowded by [X].

If we draw arc [GC] down to the line [AB] we can now use point [H] to define the fivefold division, the side of the inscribed pentagon. An arc [CH] from [C] defines points [J] and [K], which define two sides of a pentagon with a vertex at [C] as in Fig 17.

The next two divisions, two more sides of the pentagon, need to be marked off by moving the compass to the new points [J] and [K] to define [L] and [M] with arcs of radius [CH] as in Fig 18. The remaining side is exactly [LM]. This construction is geometrically exact; the pentagon is a regular polygon. This construction uses the largest number of definitions so far which require moving the steel point of the compass to a newly defined point. Very careful work is required to give the compass setting for [CH] which will exactly meet the starting point when stepped off five times around the circle.

All of the odd circle divisions technically define their multiple of two as well. This five fold division defines tenfold by extending the radii across the center to a diameter. It is not clear whether it is more accurate to extend the radii defined by the fivefold or to set up a second division by starting from [D] and drawing another fivefold division. To a large degree, it depends on your skill. What is true is that they should give the same result. If you check it and they do not agree, chase down the error before using the layout for something important.

The 20 fold division is set up with the same radius definition. A second set of divisions is started at the line [AB] 90º from [CD].

It is quite rare for all of the divisions to be exact on this one when you are finished. It is a demanding test of your skills.

iv). Approximate Constructions: 1 The Heptagon.

There is no exact purely compass and straight edge construction of the heptagon, a seven sided polygon. It is unusual to make a statement that a negative statement is proven, but a method is commonly used to prove that a particular angle or figure cannot be constructed. One exact construction was offered by the Greeks, attributed to Archimedes, but it is so obscure that it is never used. Despite this, seven and 14 arm stars and seven sided figures are uncommon but not rare in Islamic geometric art.

As remarked above, constructing a polygon in a circle is equivalent to defining the length of a side. An approximation exists for the side of a heptagon inscribed in a circle which has been known since the ancients. It was noticed long ago, probably in India, that a line segment in Fig 15, in the standard beginning layout of the pentagon and other figures, [EG] of Fig 21, is very close to the length of a side for a heptagon. It is known to have been used by the Islamic geometers as an approximation, i.e. the method was known and it was known to be an approximation.

The line [EG] is exactly Rsin60°, or the radius times one half of the chord of 120°, as it would have been known to the Greeks or Arabs. We do not need to know that to observe that it is very close to the correct length for a side of the heptagon.

If the side length [EG] determined in Fig 21 is drawn out over six sides we find that the sides are about 0.2% too short, or 0.7 mm on a 400 mm radius circle. One problem with approximate constructions is that errors add up. The errors add up to 1.2% on the seventh side and the ends do not meet. An error of 4.2 mm for one side on the 400 mm circle is a getting to be a symmetry problem. If we step off the sides in both directions from [B] as shown in Fig 23 the length error accumulates in side [MN], 6 times the error in [EG]. This is often good enough on small scale layout circles. The absolute error is very small.

Since this is an odd polygon, extending the seven radii across the circle to define the 14 fold divisions works. Stepping off a second set of sides from point [A] is sometimes more accurate than extending the radii.

On a larger scale layout this asymmetry can be redistributed, but not reduced, by extending some of the layout arcs as in Fig 25. These arcs now both step off the length of the side and define perpendicular bisectors of two of the sides. The bisectors shown now define side [MN]. The five sides in blue are now exactly equal. The length errors in sides [KM] and [JL] will be one half of the error which would have added up in line [MN] from sequentially drawn sides. This is as accurate as this simple approximation can be. For figures drawn under 200 - 300 mm radius, this is an acceptable approximation.

There are a number of more complex layouts to give slightly more accurate approximations. One construction is frequently cited as it appeals to the numerologists. The 7 polygon is created by the interaction of 4 and 3 polygons. In practice, it is sufficiently complex that it is probably not more accurate in a smaller scale real world drawing. It is interesting to look at the method. The “Four Plus Three” construction of the heptagon was developed by John F. C. Michell, a well known geometer and esotericist. For those of a numerologist persuasion, this derivation of the seven fold figure from its parts of three and four represents a certain elegance.

The derivation can be illustrated with Fig 26. The square does not need to be drawn for this but keep it in mind as you watch the construction develop. The Line [AB] is normally contained in our final figure but here it only establishes scale. The construction begins with erecting a perpendicular bisector of [AB] in Fig 27. Where the circle [oA] would cross the bisector, at [E], we define a new center. This is the center of the circle in which the heptagon is constructed. This is also the incircle of the square in figure 26. Since we don’t use the square further, it does not need to be drawn in here. The triangle defined by the points [A], [B] and [D] is the next element to construct.

The equilateral triangle defines two new points, [F] and [G], where it intersects the new circle, centered at [oo]. Two circles of radius [oF] define four sides of the inscribed heptagon of circle [oo].

Exactly as for our approximation above, adding the next sides with circles centered on [J] and [H] will result in all of the error accumulating in the last side, [KL]. Also as for Fig 25 above, the arcs defining the sides [oF] and [oG] can be extended to define the perpendicular bisectors of the sides. This gives us Fig 31, with the error shared across two sides, [JK] and [HL].

The original side length [oF] and [oG] is considerably more accurate in this approximation. The price is a bit more construction. In a real world drawing, the accuracy should be better but it is not assured. If distances [oF] and [oG] are not exactly the same, start over.

J Michell also published the same type of construction for the nonagon. The interaction of a triangle and a hexagon generates a nine sided polygon. In that case, the accuracy is not particularly good. A better approximation is presented below.

v). Approximate Constructions: 2 The Nonagon, Enneagon (Greek).

I don’t know the source for this construction but it is a reasonable approximation. As for all of the odd polygons, it suffers from the problem of stacking all of the error in the approximate side length into one edge.

construction starts, again, with the layout used in Fig 15. A perpendicular bisector of circle [oA] and a bisector of line [oB]. In this case an arc is now drawn from [A] with radius [AF] to identify a new point outside the layout circle, [G].

An arc is drawn from [G] though [A] and [B]. This cuts the line [CD] at a new point [H]. The segment [CH] is a close approximation of the side of the nonagon.

The sides are transferred around the circle as for earlier examples. An arc of radius [CH] drawn from [C] defines the first side with vertices [J] and [K] in Fig 35. Arcs from [J] and [K] define [L] and [M]. Arcs from [L] and [M] define vertices [N] and [P]. When the last two points, [Q] and [R] are defined, all of the error is accumulated in side [QR] for an error of approximately 2% of the side length, about 1% of the radius of [oA].

The same strategy used twice above can be used to split the error to sides [NQ] and [PR] at about 1% each.

This is a perennial problem for these types of constructions. The approximate constructions have small but significant errors in side length.
Due to the nature of the constructions, stepping off sides in sequence, the error tends to accumulate in one side. It is not symmetrically distributes around the polygon so it can become enough of an error to noticeably affect symmetry.

In the next post it is time to change philosophy and address the last method for constructing approximate polygons- dividers.

Notes and Curiosities;

1) A curiosity in the naming of degrees and divisions. One of the very useful results of geometry / trigonometry is that the sum of the internal angles of a triangle is 180º. In the older nomenclature, that would be three sixths. For a square the internal angles sum to four fourths. For a pentagon they sum to 15 tenths. For a hexagon they sum to 12 sixths. For a heptagon they sum to 35 fourteenths. For an octagon they sum to 24 eighths. The sum of the angles of the polygons by reference to the whole circle is therefore; triangle one half, square 1 whole, pentagon 1.5, hexagon 2, heptagon 2.5, octagon 3…..

2) Notes on Compass Use

There is an understandable tendency to think that a six inch compass (150mm) will draw a 6 inch radius circle since you can open it that far. This is not good practice as detailed below.

Opened as at the left to the absolute maximum radius, you will have two problems. It will dig a hole in the center of your drawing. The steel needle point is leaning far to the outside of the circle. The needle will tend to “skate” and you will need to press quite firmly to keep it on the center. A hole results. That same firm pressure to keep it from skating will tend to flex a poorly designed compass, creating an inaccurate circle. Most modern compasses are not well designed to handle flexing pressures. The setting at the center is better. It will not dig a hole in your center but it will still put some flexing stress on your compass. The setting on the right is best with a vertical steel point and no flexing stress on the compass. You give up almost half of the opening to use your compass correctly. The less expensive your compass is, the more important these points are. To put it another way, your compass was not designed to do what you thought. Those joints are there for a reason. If the ARE NOT there, you are even more limited.

Basic Operations with the Compass 3: Divided Circles. The Foundations of Geometric Pattern

Basic Operations With the Compass; 2 Angle Bisectors

A Compass Exercise: Precision Revealed.